In this thread, we will see how Laplace’s Law applies to medicine: From compression stockings to diverticulosis.
Pierre Simon Laplace = quite the stud. In mathematics, known for the Laplace transform (diff calc), Laplacian (Vector calc), and Laplace distribution (prob theory). But easily mixed up with Lagrange and Legendre. Why all the French “L” mathematicians in 1700s?
While unclear whether Laplace should deserve all the credit, our medical textbooks almost universally refers to it Laplace’s Law.
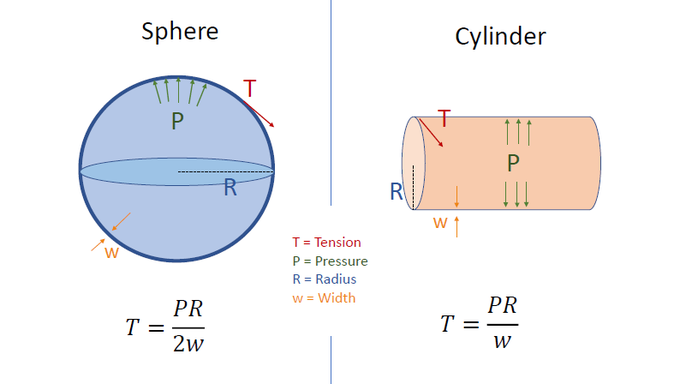
The Law describes the relationship between Pressure, wall Tension, and spherical Radius. E.g. For given R, doubling of P = doubling of T.
Laplace’s formula for a sphere’s is T=(PxR)/2. In truth, the tension is spread over the thickness/width (w) of the wall so the denominator also includes variable ‘w’. The Laplace’s formula for a cylinder is also included here.
Note: the Tension of cylinder wall is twice that of a sphere’s for a given pressure and radius. Explains why the Tension on this balloon is greatest at the cylindrical portion compared to the spherical, uninflated portion (on left).
Some really counter-intuitive aspects of this law: for a given Tension, the Pressure increases as Radius decreases.
So when you connect 2 balloons, the smaller balloon empties into the bigger one. WTF?!!
Some really counter-intuitive aspects of this law: for a given Tension, the Pressure increases as Radius decreases.
So when you connect 2 balloons, the smaller balloon empties into the bigger one. WTF?!!
6/18 pic.twitter.com/YmQKiviuGU
— Andrew C Ahn (@AndrewCAhn2) May 17, 2019
The lungs have a similar analogy (alveoli) as taught in pulm physiology.
Air would move from the smaller alveoli to larger ones, if it weren’t for the pulm surfactants (lowers surface tension for smaller alveoli).
Notice how bicycle tires inflate to 130 psi while car tires only to 40 psi. Why?
Ans: To counter orthogonal forces of pressure, much more effective to have greater curvature (smaller R). With greater curvature, more wall tension can be applied orthogonally to counter pressure
How does this inform us about compressive stockings? Accordingly, compression stockings would be more effective in generating pressure on slender legs than thicker legs (P=T/R).
So … See Slide
So how can Laplace explain diverticula?
Diverticula was practically non-existent pre-20th century. In the developed Western world, diverticula occurs primarily in sigmoid colon, more commonly with increasing age and less frequently in vegetarians (more fiber).
QUESTION: Why does diverticula occur more frequently in the sigmoid colon?
A. Larger fecal load in the sigmoid colon –> greater intraluminal pressure
B. Sigmoid colon have smaller diameter –> higher intraluminal pressure
C. More penetrating vasa recta –> more diverticula
ANSWER: (B – Correct) According to prevailing theory, sigmoid colon has a smaller diameter and thus, according to Laplace, higher intraluminal pressures (for given colonic wall tension). Furthermore, contractile rings lead to segmentation which leads to localized pressure.
Higher fiber intake leads to greater radius and thus ironically lower pressure. However, at the other extreme, too much stool leads to greater pressure and ischemia (stercoral colitis) too. So my guess: best not to have too little or too much stool/fiber in the sigmoid.
Laplace also has implications for bladder function:
Once bladder is distended beyond 400-500 cc, how effective will the contractile muscles be in generating bladder pressure to excrete urine? Not so much (P=2T/R).
Reason why catheterization is indicated in these situations.
The Law applies to other systems. Can you understand why:
-
Dilated cardiomyopathy is associated with poor myocardial circulation?
-
Esophageal varices are at increased risk of bleeding at greater diameters
-
Small arteriolar muscles are effective in controlling pressure?
Extra: For those math nerds out there (like myself), here is one way to derive Laplace’s Law.
However, these derivations demonstrate major underlying assumptions:
(1) System is at equilibrium,
(2) Wall is elastic,
(3) Pressure is constant at interval volume change, etc…
Which may not be all true in the complex body (e.g., wall can be viscoelastic, etc.)
SUMMARY:
-
Laplace describes relationship between wall tension, radius, and pressure
-
For a given wall tension, smaller radius is associated with greater pressure
-
This law has applications to multiple anatomical systems
-
Be careful not to overgeneralize given assumptions